Times here means multiplication. If you take a length of 3cm and multiply it by width of 2 cm, you are adding 3cm twice, which gets you 6cm. why is that the 'area'. Actually, what does area even mean? Of course I understand that you have to multiply the units too, so it's actually 6cm squared. But cm squared as a concept is even more baffling.

Someone explain to me like I am five the idea of area and why it's length times width.

>>16697608 (OP)
If you have a grid of finitely many dots, you find the total number of dots by multiplying the number of dots across and along. Area is just extending that for the continuous case.

>>16697608 (OP)
I feel like this is a concept that people are supposed to be taught when they're 5.
Let's say I have a square 1 unit long, 1 u wide.
Now let's say I have a second square and I put that alongside the 1st square, look at the rectangle formed from the two of them and measure it's width, it is 2 u wide, 1 u long.
Now let's say I have a different square 1 u wide, 1 u long. I put a square underneath it, now you have a tall rectangle, 1 u wide, 2 u long.
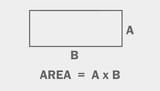
Both rectangles you just formed have the same number of squares, the area of each square that formed them is 1 u^2.
Now that you have these rectangles both formed from 2 squares of area 1 u^2, you have rectangles of area 2 u^2.
And that is the point, you can compare them. You don't care which one is longer than the other or wider than the other, you care how many squares make up the rectangles. You don't need to care about the arrangement of the final shape in order to compare things by their area. I can say the area of a circle, a rhombus, a parallelogram, I can make a closed squiggly and still find it's area, I can curve the shape in 3d space and still compare it's 2d surface area.
That's why we care about area.

Imagine a string that is 2cm long. If you stacked those strings on top of each other until it was 2cm high, the area is all those strings added together. 2cm strings stacked 2cm high gives you an area of 4cm. Also, units are not like variables in an equation that get squared when you multiply then together.

>>16697618

>Also, units are not like variables in an equation that get squared when you multiply them* together.

Spelling correction.

>>16697608 (OP)
Learn topology and measure theory. Then it becomes self-evident. You have a topological product of two closed intervals and the measure respects this multiplication.

>>16697608 (OP)
xxxxx
xxxxx
xxxxx
This is 5 x's long and 3 x's tall. There are 15 = 5*3 x's here. Hope that helps.

>>16697622
Best answer honestly

>>16697608 (OP)
When you have line A and you raise it to B you can mirror the same line on top of the existing one and get an area which is ABcm^2

>>16697608 (OP)
because it behaves like how you'd expect a mathematical concept of area to behave
specifically, if you multiply the length of one (JUST ONE AT A TIME, BUT IT CAN BE EITHER ONE) of the sides, then the area is multiplied by the same factor.
furthermore, if one of the sides is length 0, then the area is zero.

>>16697608 (OP)
This is something that should have been intuitively obvious in 2nd or 3rd grade.

>>16697610
NGL this is easily the best answer. But I don't know how the hell continuous mathematics works lol

>>16698021
OK. Explain.

You start with a bunch of tiny identical squares. You arrange these side by side to form a rectangle. You notice making a bigger rectangle requires more squares. You decide to define however many squares you need to build a rectangle as Size. So far so good. The smallest rectangle you can make is just one tiny square. You decide this has size 1. The next biggest has Size 2, and so on.

You quickly realizee that a long rectangle has the same Size as a w i d e rectangle. Placing the squares left to right, or bottom to top, doesn't change how many squares you need. Still, it would be nice to note their difference, so you keep track of how many rows and columns you need. For example for a Size 2 you could build either a 2 by 1 rectangle or a 1 by 2 rectangle. These are appreciably different, but have the same Size (2).

Now you've built a huuuuge rectangle. Big Size, of many tiny squares. How can you count all these squares to determine the Size? My god, it will take forever!

Well, fortunately your rectangles are nice, no holes, no unevenness, no gaps or out of place angles. All the tiny squares line up perfectlty.

Huh.. Well then each line of squares must have the same number of squares going left to right, so they have the same Size. And you know if you switched row and column you would still get the same Size. So you could build it up with by placing N 1 by M rectangles, or M 1 by N rectangles, so N rectangles with size M or M rectangles with size N, both for a total of M * N squares = Size A.

Now you imagine those squares are REALLY tiny...

How the hell do you not understand this??? What the actual fuck are you even doing?

>what does area even mean
what are you looking for? more words? a word salad? a mathematical definition? a physical intuition?

Area is compounded out of the ratio of the sides, think about lines k,l, and m and and magnitude as well to develop a deeper understanding of area

>>16697608 (OP)
Area is how long it is times how wide it is. What's even there to not get?

>>16697608 (OP)
Cut the rectangle into very small squares and count them, the error at the side will be smaller and smaller as the squares get increasingly smaller

>>16697608 (OP)

The way you can think about it is by asking this question: how many times does a unit square fit inside a rectangle? That is literally the definition of a surface area.

Now let's try to use an example. You have a rectangle which is 7.38 units wide and 3.61 units tall. How many times can a unit square fit inside that shape?

The side of that rectangle is 7.38 so what we are going to do is place seven unit squares side by side in a row. Then add another 0.38 of a square. Now we have created a rectangle with an area of 7.38 because we just put 7.38 unit squares side by side.

The next thing that we will do is stack those rectangles that we just made (surface area of 7.38) on top of each other. How many you ask? First we will stack three of them. Then, you guessed it: add another 0.61 of a rectangle and what we have now is a rectangle with an area of 7.38 x 3.61. See how the area of that unit square got first multiplied by 7.38 and then by 3.61 to create that original rectangle that you had, with the surface area of 7.38 x 3.61. That is how many unit squares fit inside your rectangle. It works the same way with the same logic for any rectangle with any side lengths. You just start asking how many times you put the unit squares side by side, and then you ask how many times those things go on top of each other.

Why not euclids algorithm a unique unit based on the side lengths instead of making up fake and gay units

>>16698129
this