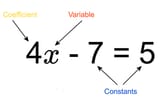
How does a coefficient differ from a variable? Terms are joined by implicit multiplication operations (so 2x^2 is just 2 * x^2), but the commutative property makes the order these appear in purely a matter of convention, so the “It’s the first number in the term” explanation is unsatisfying.

Since the coefficient value itself can be variable in certain contexts, I don’t understand what it is that makes the coefficient a coefficient.

The nearest I got to an explanation was having an LLM explain that the variable is multiplication, whereas the coefficient is scaling, but this didn’t really make any sense to me, since the operations are exactly the same.

.............
.............
.... its the number you multiply the variable by...
When you see 2x you multiply the variable by 2. Always. Its doesnt vary.

7 year olds can answer this question. Remeber that formalism is always secondary to intuition. You wont ask silly questions like this.

>>16705184 (OP)
What.
Did you, once again, get lost on your way to google?
>what's the difference
>no, I don't know what a graph is, why is there a letter here, what the fuck
Fuck off, retard.

>>16705184 (OP)
A variable, by definition, can vary. The coefficient is a constant, with a set value, so that you can establish a function.

In a expression, mx+b, m, x, and b are all variables. In order to make a function out of this, you must establish which variable it is in terms of and set constants for the remaining.
So if you want a function f(x)=mx+b, you have defined x as your variable and now must establish constants for m and b, with m being a coefficient of x.
If you were to make a function f(m), then m would be your variable and you'd have to set a constant x to be the coefficient of m.

Hope that helps.

>>16705189
>.... its the number you multiply the variable by...
This is wrong. If you had 4x^2y^2, you multiply x^2 by both 4 and y^2. The coefficient is not y^2.
>>16705196
>The coefficient is a constant, with a set value, so that you can establish a function.
This was my understanding but I read that the coefficient *isn't* always constant. This could just be wrong. Would it be accurate to say that while the coefficient can vary between functions, it's constant in the context of a specific definition of a function? So like you said, all three are variables, but m becomes a constant when we create a function where x is the variable?

We've only just begun learning this kind of stuff but my professor doesn't seem to have time to really delve into questions like this, so I appreciate your help.

>>16705200
>Would it be accurate to say that while the coefficient can vary between functions, it's constant in the context of a specific definition of a function?
Correct enough.
You seem to be quite early in your math education if you "only just begun learning this kind of stuff" so I'll tell you what I wish I knew before:
A good teacher lies to his students a little less every day. There's hard rules in math you've been taught that you'll later learn aren't nearly as universal as you were led to believe. Always remember that the teacher is really talking to the slowest kid in the class.
You can even pass one function as a coefficient in another function but that's nothing you should be worried about right now.

>>16705200
>the coefficient is not y^2
You said it yourself retard.

You dont even have a claim or a question here. You are just failing to grasp the most basic concepts in math and calling it rigor.

>>16705206
>Always remember that the teacher is really talking to the slowest kid in the class.
Yes, she's very patient with me. Cheers.
>>16705208
> You said it yourself retard.
Based off of convention, not an actual definition. Your definition was nonsensical so it doesn't appear that you understand it, either.

>>16705212
4x^2y^2 is by definition 4*x^2*y^2. If you cant tell if 4 is a variable then you are literally retarded.

Dont bother thinking about multivariable equations because you wont possibly progress that far.

Give me one example where it is any way ambiguous whether 4 is a fucking variable or not. Lol.

>>16705184 (OP)
>filtered by pre-algebra lmao

A coefficient is a constant multiplied to a variable. Stop posting here until you are 18.

>>16705219
4 is not a variable, but you didn't include "constant" in your original definition. It can't just be "the number you multiply the variable by" because you can have terms with multiple variables that are *also* numbers which are *also* multipliers of other variables in the term.

>>16705233
There still isnt any ambiguity because all constants will compose into a single constant. In any expression of that form there is at most one constant, the coefficient.

>>16705242
That is helpful, thank you.

Here's a fun one.
2^3^2 =

(A) 2^(3^2) = 2^9 = 512
(B) (2^3)^2 = 8^2 = 64

Another one:
4*5^3 =

(A) (4*5)^3 = 20^3 = 8000
(B) 4*(5^3) = 4*125 = 500

PEMDAS
PEMDAS is an acronym used to mention the order of operations to be followed while solving expressions having multiple operations. PEMDAS stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction. There are different acronyms used for the order of operations in different countries. For example, in Canada, the order of operations is stated as BEDMAS (Brackets, Exponents, Division, Multiplication, Addition, and Subtraction). Some people prefer to say BODMAS (B- Brackets, O- Order or Off), while few others call it GEMDAS (G- Grouping).

Here's a breakdown of the PEMDAS rules:
Parentheses (or Brackets): Work on the expressions within parentheses, brackets, or other grouping symbols first. If there are nested parentheses, start with the innermost set.

Exponents: Next, calculate any exponents (powers or roots).

Multiplication and Division: Perform multiplication and division from left to right.

Addition and Subtraction: Finally, perform addition and subtraction from left to right.

>>16705219
> 4x^2y^2 is by definition 4*x^2*y^2. If you cant tell if 4 is a variable then you are literally retarded

If we follow PEMDAS RULES OF OPERATIONS.
Let's insert parentheses.

4*x^2*y^2
4*(x^2)*(y^2) powers are done first (left to right)
You see, unfortunately, people wing it in all walks of life these days. In some ways, Reverse Polish Notation works better, but it'd be better if they taught kids to add clarifying parentheses. Downside is a lot of Algebra gets harder if you do that after the fact.

Going to be honest, not sure what you're struggling with here. 7, 5, and 4 are all constants, and x is a variable. 4 is a constant coefficient of the variable x. in this >>16705200 example, 4 is the constant coefficient for the variables x and y. A coefficient is a constant multiplied by at least one variable. This isn't rocket surgery.

>>16705200
A general form exists for a relation where coefficients are listed as a variable form, but they are not variables. In real uses, these coefficients are parameterized based on the actual condition. Many closed solutions have such things in math. Programming also has this form.

>>16705277
It’s A) in the first one. Power of a power rule.

>>16705184 (OP)
4 ~= 4\alpha

Just use substitiution

5x + 3 = 7
y + 3 = 7

so y = 5x
therefore 5 is a coefficient

>>16705184 (OP)
I read that the coefficient is a number that is constant in certain contexts.

the best I can think of is Beer's law (in analytical chemistry), where e * p * c = absorbance. c is analyte concentration, p is path length of light through the solution, and e is the extinction coefficient, which depends on what analyte is used. for a given analyte e will be constant, but between different analytes e is variable.

a true constant would be pi and euler's number.

>>16705223
in a linear equation Y = ax + b the b is not multiplied by any variable but is still called a coefficient

>>16707176
If you wanna bang on technicalities, a linear function is a first degree polynomial and b is a coefficient of x^0. This isn't even a trivial statement. There are cases where this fact must be held true and understood to maintain consistent definitions as you go deeper in your study of math.

>>16707200
in that case can't you say that every constant in an equation is a coefficient, as they can all be expressed as "constant * x^0"

>>16707213
Now you're getting it.
These things are all context dependent. Rigorous definitions exist in math but if you're at the level where this concept is confusing for you, then it's good enough that you are capable of pointing at a number in an expression and correctly stating "this is a coefficient of x" or "that is a constant." The goal being that you're able to look at a function's equation and determine some things about its behavior before you ever put pen to paper.