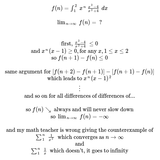>math problem in class
>come up with a different solution but same answer
>teacher says it's wrong and gives a counterexample
>be not convinced
>let is pass because social anxiety
>three months later, remember you're still not convinced
>spend 2 hours learning and typing latex so /sci is happy
Please tell me I'm right

>>16710441 (OP)
You are wrong and your teacher was right. Just because something is decreasing doesn't make it converge to -infinity.
I don't understand what you don't understand about your teachers explanation.
Your argument literally seems to be
>f(n) is decreasing
which is correct
>therefore lim f(n) = -infinity
which is false.

>>16710441 (OP)
nigga never heard of asymptotes lmao

>>16710441 (OP)
how can f(n) not go to -infinity if it keeps decreasing?
It has no limit but is decreasing, it never stops, but it accelerates downward. And the acceleration accelerates downward. And so on.
The limit is -infinity because there is no one value that it stops at

>>16710452
that would be right if the the function didn't have increasing decrements

>>16710444
>>16710452
it's intuitive, try to read the differences part and sleep on it and come back

>>16710441 (OP)
I have faith in you retards
Don't make me go to poopy reddshit

>>16710470
It’s what again, sweetheart?

>>16710441 (OP)
>Please tell me I'm right
despite the counterexample?

I think your argument is fine, maybe could be written more clearly. Like it took me a sec to see why you were writing x^n(x-1)>=0 when the point is just to show that x^n is decreasing with n on that interval of x, so I recommend that you always try to be as clear as possible. But you are correct, not sure why everyone is ignoring the "differences of differences" argument and bringing up asymptotes when you covered that.

>>16710501
Nice try but weierstrass doesn't work for functions where I can make my picrel argument. The decrements increase at all levels. The function can't slow down because there's not a negative acceleration at any level.

>>16710503
The facts are right in the counterexample but it doesn't apply here. It went over the teacher's head

>>16710507
Love you

>>16710441 (OP)
Who cares about that math shit

>>16710509
2^-x is a strictly decreasing function, but it doesn't decrease to -inf

>>16710509
The fact that you use terms like “slow down”, “accelerate” and “intuition” tells me you’re a physicist taking baby’s first analysis course.

So, in proper language, you’re saying a monotonically decreasing function whose domain is the entire R, or at least some open ray (a,infty), with an everywhere-non-negative second derivative must diverge to -infty.

I don’t even understand your teacher’s counterexample because you have a sum from 1 to n of x^-2, which is just nx^-2, but then you make it a function of n? That would make the second derivative vanish. You need to work on your notation and communication, whether you’re right or wrong. You probably said something incoherent to your teacher, he interpreted it in a way different from yours, and then gave you a different counterexample to an entirely different claim.

>>16710441 (OP)
f(n) ≈ int[1,2] (-x^n) for large n, which obviously goes to -∞

>>16710526
But it slows down

>>16710528
Plain actual retard
But my point is all degrees derivatives are everywhere-non-negative
And I finished highschool just now and going into economics

>>16710531
You're right, that's even simpler
But nobody would even care if I said an approximation

>>16710540
>calls me a retard despite not being able to communicate properly
>uses dogshit notation like [math]\sum_{1}^n 1/x^2[/math] (that's just nx^{-2} lil' bro)
>boasts about outdoing his math teacher (the teacher didn't understand him)
Yep, a classic economics student. Take undergrad analysis just for shits and giggles while you're at it, anon. It humbles you down.

>>16710545
You're sad
>calls me sad despite not being able to communicate properly
>Muh communication
I'd rather be a genius than able to share my ideas

>>16710560
Please apply your genius to economics and steer clear of math. Thank you. You still haven’t adressed the retarded way you wrote nx^-2 lel.

>>16710570
>says to be more explicit
>condemns more explicit option
>no other arguments
Ha. I win

>>16710590
>[math]\sum_1^n 1/x^2[/math] is more explicit than [math]n/x^2[/math]
I kneel to such genius. Truly, the Gauss of our times.

>>16710441 (OP)
Your reasoning is incorrect. But the counterexample that your teacher gives doesn't work. The real counterexample is f(n) = 1/n, which is strictly decreasing but the limf(n) = 0. If you need an example where f(n) < 0 for all n, then consider f(n) = (1/n)-2. Then f(n) is strictly decreasing, but lim f(n) = -2.

>>16710600
Your counterexample slows down in its descent. Take -x or -x^2. The OP function doesn't work like 1/n

>>16710624
> slows down in its descent
You must make this mathematically rigorous. We are not dealing with speed or velocity. this isn't physics. Use derivative language.

>>16710643
I'm just an intuitive boy, I need no sympathy

>>16710656
>I need no sympathy
oh, don't worry, you won't get it

>>16710441 (OP)
[math]\sum_1^n \frac{1}{x^2}[/math] does not converge as [math]n\rightarrow \infty[/math]. You probably meant [math]\sum_1^n \frac{1}{n^2}[/math] and [math]\sum_1^n \frac{1}{n}[/math].

>>16710879
[eqn] \lim_{n \to \infty} \sum_{x=1}^n \frac{1}{x^2} =\zeta(2) = \frac{\pi^2}{6} [/eqn]

>>16710905
So after like what, 30 posts itt, OP finally explains his dogshit notation. So we’re dealing with a function with integer domain and real codomain. And the claim in OP’s pic is that if it is (non-strictly) monotonically decreasing (as f(n+1) <= f(n)), then its limit at infinity is -infty. But then somewhere along the line OP also inserted some kind of finite-difference equivalent of the absolute value of the second derivative being monotonously decreasing?

You will have a stunning career as an economist, my dude. You are only 18, but have already perfected the art of muddying the waters. You also have the characteristic boastful arrogance about it. You’ll feel at home in the econ department.

First off your argument for why f(n) is decreasing is very convoluted. The integrand is always negative with x \in [1,2] and increases in absolute value with n. Find a better way to formalize that without detours.

Secondly you provided no evidence that f(n) does not "slow down". You need to do find out the leading order behavior. Just because it decreases doesn't mean it doesn't slow down at all. Time to put your big boy pants on and actually learn analysis?

I take back what I said, you were right OP. You took the difference f(n+1)-f(n) and factored to get
[eqn] f(n+1)-f(n) = \int_1^2 x^n (x-1) \frac{x^2-4}{x^+4} [/eqn]
This in one step shows that f(n) is not only decreasing, but that each difference f(n+1)-f(n) itself is decreasing, such that it definitely does not "slow down". Good work. You were right, the teacher wasn't.

>>16710441 (OP)
This thread saddens me. Is the god damned limit not -inf?
I don't care about this or that argument and muh teacher, the limit seems bloody simple to me.

>>16710915
that's not me, I can't get mathjax to work

>>16710935
Intuitives Assemble

>>16710444
>Just because something is decreasing doesn't make it converge to -infinity
/thread

>>16710879
>>16710905
Yeah, that's what I meant, I fucked up the notation just like OP.

If f'(x) < 0 at least almost everywhere then surely f(x) diverges to negative infinity

>>16710935
Find the upper bound of a subinterval and show that goes to -inf

>>16711788
f(x) = e^(-x) is a simple counterexample for your claim.

>>16711800
[math]\int_{1}^{1.5} x^n \frac{-7}{25}[/math]

>>16710441 (OP)
f(1/0) = –1/0
f(1/0 + 1/2)/f(1/0 – 1/2) = 2

>>16711811
f(x) = 1/e^x > 0 for all x since e^x > 0 for all x
f'(x) = --1/e^x thus < 0 for all x

damn you are right
what other condition might we add?
I notice f''(x) = f(x) again > 0

what if we require f''(x) < 0 for all x?

>>16711811
What if -f'(x) > sigma for all x > N
where sigma > 0 ?