Is there any convenient equivalent of quaternions for 2D graphics (i.e. storing rotation and translation in a more compact way than homogeneous matrix with the 001 row/column trimmed)?

I was looking into dual complex numbers, which some page (not posting link, you can find it easily if you google that term) claims can be used like this with transformation encoded in a product, but unless I'm misunderstanding something it does not seem to fully work.

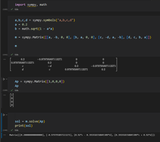
For one, they seem to be mapping to 2x2 matrices rather than 3x3. Also inverses seem to not reliably exist, even when the rotation part is normalized. You can see pic rel, where I've used multiplication rules to get a system of equations for all components of the product of two dual complex numbers and required that the product is (1, 0, 0, 0) to find the inverse. I would expect the inverse of translation components to be simply the negated original translation (as is given online), but you can see it is a function of both translation components (c and d).

Should I just give up and store a complex number / angle and translation separately?

Of course I meant dual quaternions in first post, I'm aware that complex numbers are equivalent to usual quaternions for 2D.

>>16710956 (OP)
SO(3) is isomorphic to Sp(1), which is the group of unit quaternions.
SO(2) is isomorphic to U(1), which is the group of unit-modulus complex numbers.
>Should I just give up and store a complex number / angle and translation separately?
Yes. SO(2) is Abelian and compact and all such groups are isomorphic to either SO(2) or U(1), which are basically the same due to Euler's identity.

>>16710981
*their Lie algebras are isomorphic
SO(3) and Sp(1) have different fundamental groups

>>16710981
Thanks.