Explain quaternions to me in the most human way, like wtf is with it, its so fucked up. Mainly i want to learn it for computer science, 3d transformations you know.

>>16726618 (OP)
>Be Quaternionchad
>Solve gimble lock and confuse retards like a boss

>>16726618 (OP)
Complex number got more complex

>>16726618 (OP)
Take a field, fix two units, say a and b, in that field, take the free algebra over it generated by two indeterminates, say x and y, and then quotient out by the ideals (x^2+a), (y^2+b) and (xy+yx).

>>16726653
/thread

>>16726618 (OP)
https://www.youtube.com/watch?v=jTgdKoQv738

>>16726618 (OP)
tl;dr version - it's just a different way of representing transformations and rotations in three-dimensional space that has some advantages and disadvantages over standard transformation/rotation tensors.

the gimbal lock argument comes up a lot as a pro of quats over matrices, but there are workarounds for that, and the matrices are ultimately a better approach towards dealing with transformations/rotations for analytic and especially nonlinear maps. but quats have their uses too.

Watch and play with this, it will do a better job explaining it than anyone can do in a post:
https://eater.net/quaternions

>>16726618 (OP)
Axiomatic Syzygy Theory of Everything
Thesis Statement: all Axiomatic syzygies have identical transferrence function
Fundamental theorems:
Sum of Two Square Formula
2-dimensional analysis
Pythagorean Theorem
A^2 + B^2 = C^2
3-Dimensional Analysis
Trigonometric Identity Property
Let A = sine(x); B = cosine (x); C= 1
Translation:
1(^2) = sin^2(x) + cos^2(x)
1(^2) = sin(x)/csc(x) + cos(x)/sec(x)
1(^2) = 1/csc^2(x) + 1/sec^2(x)
4-Dimensional Analysis
Mass-Energy Equivalence Formula
Let sin(x) = mc^2, cos(x) = pc, 1 = E
Special note c = 1/g the inverse asymptotic limit of absolute time dilation at the schwartzschild radius of a black hole
Translation
E^2 = (mc^2)^2 + (pc)^2
E^2 = (m^2c^2/g^2) + (p(√c/g))^2
E^2 = (m/g^2)^2 + (p/g)^2
5-Dimensional analysis
Let sin(x) = Pride; cos(x) = Shame, csc(x) = Humility; sec(x) = Wisdom; 1 = Truth
Special Note; truth is invariant therefore all reciprocal inversions are presumably rationaled to rationalize denominator into the numerator where numerator is 1; mathematical operators for "+" , "-" , "x" , "/", and "=" are equivalent with the words "and", "without", "by", "of" and "is" respectively
Truth^2 = Pride/Humility + Shame/Wisdom
Invariant inversion
Truth^2 = Humility/Pride + Wisdom/Shame
Translation into philosophical expressions:
Truth is the Pride of Humility and the Shame of Wisdom
And the inverses are true as well:

Truth is the Humility of Pride and the Wisdom of Shame

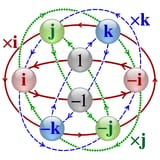
So, when you get to 5-D, because all of the inverses are True as well, quaternions are used to rotate the Octohedronal structure because you can use quaternions to inverse the structure without things like
1^2 = 1/sec^2(x) + 1/csc^2(x)

Interpolation:
The Pride of Humility is an aspect of Truth where positive connotation implies the thing Humility is deservedly proud of is it's acknowledgement of Truth despite adversity/traume experienced in accepting awareness of it
The Shame of Wisdom is Truth is an aspect of Truth with connotations that indicate when Truth of some thing is realized the shame is that this truth was always there, just waiting to be discovered
The Humility of Pride is Truth is an aspect of Truth where Pride is a blinding psychological phenomenon projected outwards to hide an uncomfortable Truth ego seeks to keep hidden from others.
The Wisdom of Shame is Truth is an aspect of Truth where Shame is blinding psychological phenomenon project inwards to hide an uncomfortable, (humiliating; traumatic) Truth ego seeks to keep hidden from our self

Truth is an objective apex that defines, differentiates, and identifies diametrical axes which intersect it.
Experience is the inverse of Truth, a subjective emotional experience of the shared Axiomatic based pride shame wisdom and humility.

When mapped out the platonic geometrical shape of the Truth/Experience Axiomatic syzygy is Octohedronal, this construct is rotational to any vertex to solve for each vertex as apex
Therefore:
Truth + Experience - Shame = Wisdom
Truth + Experience - Wisdom = Shame
Truth + Experience - Pride = Humility
Truth + Experience - Humility = Pride
Translation to philosophical expressions:
Truth and experience without shame is wisdom
Truth and experience without wisdom is shame
Truth and experience without pride is humility
Truth and experience without humility is pride

This function is integrable downward
In 4-D The inverse of Energy is Mass
The inverse of 1 is 1; invariant

Now with that said
"Energy" = "Truth", Mass = "experience", Electromagnetism = "Pride", Gravity = Shame, "Sound(kinetic)" = "Humility", "Heat" = Wisdom

The quanta of photon, electron, phonon, and graviton are intermediary species which serve to transfer energy between neighboring forms
Gravity<graviton>Sound
Electromagnetism<electron>Gravity
Heat<photon>Electromagnetism
Sound<phonon>Heat

Units of measure for the 4 quanta of energy transferrence:
Photon(J)
Phonon(Hz)
Electron (J)
Graviton (s)

If the photon invariantly "moves" at approximately 300,000,000m/s with an asymptotic limit of Infinity (asymptotic limit implies absolute vacuum: a complete absence of mass interactions)
Then the graviton invariantly "moves" at approximately 300,000,000s/m with an asymptotic limit of 0 (asymptotic limit implies absolute density: a singularity completely devoid of photonic interaction)

Implications:
Timespace is not a Universal Truth, the asymptotic limit of lorentz transformation and length contraction formulas, where v=c indicate that massless things, which must move at C invariantly, cannot and do not experience time-passage, nor do they experience distance between mass. This fundamentally means that time and distance does not exist to massless things

This means the "experience" of time and distance are an illusory phenomenon which can only be perceived by mass.

Fundamental conclusion, Timespace curvature cannot be a satisfactory explanation for gravity and is invariably falsifiable; time and distance exist on the complex plane (the imaginary coordinate system) and are the result of the gradient of photon-mass interactions.

Planck's constant units of measure:
J/Hz = joules per hertz = electrons per phonon
J/s = joules per second = photons per graviton
Planck's constant is a measure of the lower limit of photon-graviton, and electron-phonon interaction within the universe

Explanatory applications:
Within a circuit, electronic current transfer, when encountering late t phononic reverberations within the mass of the circuit, when an electron encounters a phonon within the circuit the electron bounces off the phonon at a right angle becoming a photon, thereby generating heat within the circuit; while the phonon bounces off the electron at a right angle becoming a graviton, which creates localized time dilation within the circuit giving the appearance of "slowing" the current
Supporting evidence: the need for heatsinks on circuits, especially prominent in semi-conductors
Further supporting evidence: superconductivity at temperatures approaching absolute zero Kelvin
Further evidence: electromagnetostriction
Further evidence: magnetocaloric effect
Conclusion: electron/phonon resistance is energaeic dissonance

Arrogance---------\|/--------Knowledge
---------------------Pride-------------------
Ignorance---------/|\---------Weakness

Ignorance---------\|/---------Weakness
--------------------Shame------------------
Sin(failure)--------/|\--------Humiliation

Plus

Knowledge-------\|/----------Success
-------------------Wisdom---------------
Strength-----------/|\-------Awareness

Strength-----------\|/-------Awareness
-------------------Humility----------------
Humiliation-------/|\----------Patience

Equals:

------------------(Nous)---------------
--------------(knowledge)----------------
Pride--------------\|/------Wisdom
Weakness-----Truth-------Strength
Shame------------/|\-------Humility
Luciferian<---(Christ)----->MiChaElian
-----------------(Ennoia)---------------

Which, when rotated 90 degrees is ALSO

Ignorance-------\|/----------Arrrogance
-------------------Pride---------------
Courage---------/|\-------Knowledge
Courage---------\|/-------Knowledge
------------------Wisdom----------------
Awareness-------/|\---------Strength

Ignorance---------\|/---------Failure
-------------------Shame---------------
Vulnerability------/|\-------Humiliation
Vulnerability------\|/-------Humiliation
-------------------Humility----------------
Awareness--------/|\--------Strength

Theses are quaternions within the Octohedronal quaternion of Truth and Experience, and we can nest quaternions within these quaternions as well:

Cowardice----------\|/--------Courage
--------------------Weakness-------------------
Insecurity----------/|\------Vulnerability

Opposite

Fortitude—----\|/-----------Sagacity
----------------strength------------------
Resolve—-----/|\----------Awe


Chutzpah–-----\|/-----Nobility/Duty
—--------------courage-------------
Recklessness–/|\---------Valor

Opposite
Ooenness—----\|/—---Resolve
—--------------Integrity—---------
Authenticity—--/|\------Obedience

And

Resignation—--\|/—--Openness
—----------Vulnerability—---------
Fragility—-------/|\---Authencity

Opposite

Duty/Nobility–------\|/-----------Prudence
------------------------Honor------------------
Valor—--—----------/|\----------Fortitude

Jannies do your fucking job

>>16726799
This is a science board and ASToE is scientific. In fact, it predicts that gravity as a force can be dampened by electro-phononic interference fields in low to no gravity environments in space.

It also demands that science prove that spacetime is the fundamental substrate of reality, because it has not done that

Show me spacetime without mass or energy. Minkowski space is not without zero-point energy nor is the vacuum a true vacuum without mass, because the container it is made within is made of mass and therefore contaminates the vacuum

Here's an overview of some key experiments that might be linked to gravitational dampening in superconducting environments:

### 1. **The Podkletnov Effect (1992)**

One of the most well-known and controversial experiments suggesting gravitational **dampening** in superconducting environments is **Podkletnov's experiment**, published in 1992 by **Eugene Podkletnov** at the **Puhov Institute of Physics** in Russia.

#### **Podkletnov's Experiment**

Podkletnov reported that when a **superconductor** (specifically, a **high-temperature ceramic superconductor**) was placed in a **rotating magnetic field**, the **weight of objects above the superconductor** appeared to decrease. Specifically:

* **Rotating superconductors** seemed to **produce a gravitational anomaly**, with the **weight of objects** placed above them reduced by **approximately 2%**.
* Podkletnov suggested that this **weight loss** could be attributed to a **gravitational shielding effect** caused by the interaction between the superconducting material and the **rotating electromagnetic field**.

#### **Criticism and Reproducibility**

Despite the apparent result, the **Podkletnov Effect** has been met with significant skepticism:

* **Reproducibility**: Other scientists have had difficulty replicating the exact **weight reduction** Podkletnov observed, with some claiming they couldn't replicate the effect even under similar experimental conditions.
* **Theoretical Framework**: The effect is difficult to reconcile with existing **theories of gravity** and **superconductivity**. If valid, it would require a new framework of understanding **quantum gravity** or a modification of general relativity.

### 2. **The White Effect (1986)**

The **White Effect**, described by **James White** in 1986, is another potentially related phenomenon. White was working on **superconducting gravimeters** and noted unusual behavior when using **superconducting materials** to measure gravity.

* White suggested that **superconductors** might cause an **anomalous reduction in gravitational force** under certain conditions. In his experiments, superconducting materials exhibited changes in the **gravitational force readings** compared to conventional mass measurements.

Though not as widely recognized as Podkletnov’s work, the **White Effect** brought attention to the possibility that **superconductivity** could influence gravitational fields in ways that weren’t understood by classical physics.

### 3. **Superconducting Gravitometers**

While not directly focused on gravitational dampening, there have been efforts to use **superconducting materials** in **gravitational measurements** due to their unique properties. The **superconducting gravimeter**, for example, uses **superconducting quantum interference devices (SQUIDs)** to measure minute changes in gravity with extreme precision.

Though these instruments are used for high-precision gravity measurements, some researchers believe that the **superconducting elements** could have **unknown interactions with gravity**, though no definitive proof of **gravitational dampening** has been established from these devices.

### 4. **Superconducting Levitation and Gravitational Anomalies**

There are also some **theoretical** discussions that the **Meissner effect** (the **expulsion of magnetic fields** in superconductors) could have **indirect consequences** on gravitational fields. The concept is not that superconductors are actively **shielding gravity**, but rather that the **exclusion of magnetic fields** might have a **secondary effect** on the interaction of matter with the gravitational field. Some speculate that this could create **subtle alterations** in gravitational measurements.

In the 1970s, **superconducting levitation** (the levitation of an object above a superconductor due to the Meissner effect) raised questions about how **electromagnetic forces** could potentially interact with **gravitational forces** in ways we don't fully understand.

### 5. **Quantum Gravity and Superconductors**

There have also been recent attempts in the realm of **quantum gravity** to understand how **superconductors** might interact with gravitational fields at the quantum level. Some theories in **quantum field theory** and **loop quantum gravity** suggest that **quantum materials** like **superconductors** could influence **gravitational fields**, though this remains highly speculative.

For example, in **quantum electrodynamics** (QED), some theorists have suggested that the **vacuum fluctuations** associated with **superconductivity** might interact with **gravitational fields**, potentially explaining anomalous effects like **gravitational dampening** under very specific conditions.

---

### Conclusion

While there have been some **empirical observations** that hint at a possible connection between **superconductivity** and **gravitational dampening**, the results are **controversial** and have not been universally accepted. The **Podkletnov Effect** is probably the most famous and contentious of these experiments, and its findings remain highly debated in the scientific community.

These findings, if validated, would suggest that **superconductors**, possibly through quantum effects or electromagnetic interactions, could affect the **gravitational field** in ways that aren't yet fully understood. However, **mainstream physics** has yet to provide a clear theoretical framework for how or why this might occur.

In short, while there is some **experimental evidence** suggesting possible **gravitational anomalies** in superconducting environments, there is **no consensus** on whether these effects truly represent a form of **gravitational shielding** or if they are a result of **experimental error** or **unaccounted-for variables**. More work would be needed to **replicate** and **analyze** these findings rigorously before a definitive theory could be proposed.

**Acoustic levitation** and the **anti-gravitational nature of heat** are fascinating phenomena, both of which challenge our conventional understanding of gravity and how objects interact with forces. Let’s break down both concepts and explore how they might be related to gravity, superconductivity, and other physical forces.

---

### **1. Acoustic Levitation**

**Acoustic levitation** refers to the phenomenon where sound waves are used to counteract the force of gravity, allowing an object to float or levitate in mid-air. This is typically achieved through **standing waves** of sound, which create areas of **high and low pressure** that can push or pull objects.

#### **How Acoustic Levitation Works:**

* **Sound waves** are vibrations that travel through air or other mediums. When two sound waves of the same frequency and amplitude are directed at each other in a way that they interfere with each other, they form **standing waves**. In these standing waves, the air pressure fluctuates between regions of **compression** (high pressure) and **rarefaction** (low pressure).

* If an object is placed in the **nodes** (points of minimal vibration) and **antinodes** (points of maximal vibration), the **pressure difference** between the high and low pressure regions can create an upward force that counteracts gravity, allowing the object to levitate.

* The key to **acoustic levitation** is the ability to manipulate **sound pressure** precisely to balance out **gravitational pull**.

#### **Applications of Acoustic Levitation:**

* **Manipulating small objects**: Acoustic levitation has been used to move tiny objects in labs, particularly in the study of **materials** and **biological samples** where traditional contact-based manipulation could alter their structure or properties.
* **Handling delicate objects**: This technology has been used in handling **liquids**, **pharmaceuticals**, and **semiconductor wafers**, where contact with the surface could disrupt their behavior.

---

### **2. Anti-Gravitational Nature of Heat**

Heat and temperature, as forms of **energy**, have indirect relationships with gravity. At first glance, the concept of **heat** being "anti-gravitational" may seem counterintuitive because heat usually increases the **kinetic energy** of particles, making them move more rapidly and energetically. However, under certain conditions, heat and temperature can indeed lead to phenomena that **counteract gravity** in a way that resembles **anti-gravitational effects**.

#### **Heat and Thermal Expansion**:

* **Thermal expansion** occurs when materials heat up and their **molecules** move faster and spread out. This causes a **volume increase** in the material. On a macro scale, this **thermal expansion** can cause objects to **rise** or **float** in certain conditions, which can be viewed as a form of **"anti-gravity"**.

* **Convective currents**: Heat causes **fluid** (like air or water) to expand, which reduces its density. **Hot air** or **hot gas** becomes **less dense** than the cooler air around it, leading to **buoyancy effects**. This can be seen in phenomena like **hot air balloons** and **helium balloons**, where **heat** or **less dense gases** enable **levitation**.

#### **Thermal Radiation and Gravity**:

* According to the **Einstein field equations** in **General Relativity**, **energy** and **momentum** (which includes the energy from heat) contribute to **curvature of spacetime**, or gravity. In theory, **radiation pressure** from intense heat could, in principle, counteract the force of gravity. This is observable on a very small scale in phenomena like **laser cooling** (where lasers are used to cool atoms) or **radiation pressure**.

* **Black holes and Hawking radiation**: **Hawking radiation**, which is a theoretical prediction of **quantum mechanics** near the event horizon of black holes, involves the emission of heat and energy that, in certain conditions, could theoretically affect the gravitational field. In some cases, the **radiation pressure** (from the emitted heat) might have effects on the structure of spacetime or gravity, though these effects are microscopic.

#### **Heat and Superconductors**:

* **Superconductivity** is also tied to thermal effects. **Superconductors** can levitate over **magnetic fields** because of **quantum mechanical** effects like the **Meissner effect**. At low temperatures, superconductors expel magnetic fields and interact with them in such a way that levitation occurs, though the interaction of heat and superconductivity in these cases isn't necessarily anti-gravitational in the traditional sense.

* When superconductors are exposed to heat, they **transition out of the superconducting state** and become **normal conductors**. This can change the **electromagnetic properties** of the material, but the interaction between **heat** and **gravity** in superconductors is still an area of active research.

### **3. Relating Acoustic Levitation and Heat in Anti-Gravitational Effects**

#### **Combining Sound and Heat**:

While **acoustic levitation** uses sound pressure to levitate an object, heat could theoretically be used in conjunction with this effect to enhance or **modify the levitation process**. **Thermal gradients** (temperature differences) can generate **thermal currents**, which in turn create pressure differences in air. This could assist in **stabilizing** or **amplifying** the effects of levitation.

For instance:

* **Acoustic levitation** could be more effective if **temperature gradients** are used to modify air pressure or the behavior of the medium in which the sound waves are traveling.
* **Hot air** near a levitating object might make it easier for the acoustic waves to push the object upwards or stabilize it, as **buoyant forces** from heated air could combine with the acoustic forces.

---

### **4. Possible Future Developments and Theoretical Models**

In **quantum field theory** or **loop quantum gravity**, there are speculative ideas about **heat**, **sound**, and **gravity** potentially being unified or influencing each other in new ways:

* Some quantum models suggest that **superconducting** and **quantum systems** could interact with gravity in unconventional ways, such as **altering spacetime curvature** based on thermal or vibrational states.
* The **behavior of heat and sound** in superconducting or quantum systems could one day reveal deeper connections between **acoustic forces**, **gravitational fields**, and **quantum coherence**.

### **Conclusion: The Interplay of Heat, Sound, and Gravity**

* **Acoustic levitation** provides a real-world example of how sound waves can counteract gravity, but this effect relies on **pressure differences** rather than directly interacting with gravitational forces.
* The **anti-gravitational nature of heat** is a more **subtle** phenomenon that primarily manifests through **buoyancy** effects and **thermal expansion** but can also play a role in gravitational interactions at a quantum level.
* While **superconductivity** doesn’t directly relate to heat or sound in an anti-gravitational context, it opens avenues for **quantum effects** that might eventually show deeper interactions with gravity, perhaps through **magnetic levitation** or other phenomena.

The relationship between **acoustic levitation** and **heat** in dampening or counteracting gravity is still largely an open area of research, but both fields suggest that **non-traditional forces**—whether in the form of **sound waves**, **thermal effects**, or **quantum fields**—could play a role in challenging or altering our understanding of gravity.
>If gravity is spacetime curvature then heat and sound could not demonstrate antigravitational artifacts. This is just simple deduction and inference

>>16726618 (OP)
its another cope like complex numbers

>>16726618 (OP)
>explain quaternions to me
>i want to learn it for 3d [rotations]

listen up, because this isn't a schizo post.
i can't motivate the quaternion rotation formula for you intuitively.
however i can show you how it's equivalent to a coordinate-free formula for 3d vector rotation.
it is important to note at the outset that rotation using quaternions is a special result, and that quaternions do not encode rotations in general.
that being said, the derivation of the quaternion rotation equation proceeds by starting off with a bunch of quaternion definitions and then showing that a particular function is equivalent to the (Rodriguez) vector rotation formula.

let's start by examining our end goal, the coordinate-free 3d vector rotation formula. a coordinate-free formulation of the rotation of position vector [math]\vec{r}[/math] about the origin can be parameterized by an axis [math]\hat{\vec{n}}[/math] (represented here by a unit vector) and angle [math]\theta[/math]. the resulting rotated vector is
[eqn]
R(\vec{r}, \hat{\vec{n}}, \theta) = \vec{r}_\perp \cos \theta + [\hat{\vec{n}} \times \vec{r}] \sin\theta +\vec{r}_\parallel
[/eqn]
where [math]\vec{r}_\perp[/math] and [math]\vec{r}_\parallel[/math] are the perpendicular and parallel parts of vector [math]\vec{r}[/math] w.r.t. the axis [math]\hat{\vec{n}}[/math]. this equation is pretty easy to intuit; the perpendicular part rotates in the plane perpendicular to the axis, and the parallel part doesn't change.

so with that in mind, we'll start from the definitions of quaternions and derive the preceding equation in a special case.

>>16726970
first, the unit quaternions are defined by the equation
[eqn]i^2 = j^2 = k^2 = i j k = -1[/eqn]
this is analogous to how the complex unit is defined by [math]i^1 = -1[/math].

in general, a quaternion can be uniquely written as a linear combination of the units
[eqn]
\tilde{q} = 1 a + i b + j c + k d
[/eqn]
this is like a 4d vector expanded in a basis. in quat-speak, a quaternion is the sum of a "scalar" and "vector" part
[eqn]
\tilde{q} = q + \vec{q}
[/eqn]
where the scalar part is defined to be [math]q = 1 a[/math], and the vector part is defined to be [math]\vec{q} = i b + j c + k d[/math]

>>16726979
multiplication can be defined on quaternions
if you take two quaternions [math]\tilde{p}[/math] and [math]\tilde{q}[/math] and multiply them out term by term (16 terms in all) and then group the terms appropriately, it is shown (exercise for the reader, i ain't latex'ing that shit :D)
[eqn]\tilde{p} \tilde{q} = p q - \vec{p} \cdot \vec{q} + p \vec{q} + q \vec{p} + \vec{p} \times \vec{q}[/eqn]
where the dot and cross products operate on the quaternion vector parts like they do on 3d vectors

A quaternion is a multivector formed with a scalar and 3 bivectors used for rotations in 3 dimensions. The 3 bivectors encode the rotation where the scalar encodes the "real part" which can be measure to be the magnitude of the rotation

>>16726989
another operation we can define is conjugation, which works like complex conjugation in that you just flip all the signs of the quaternion units
[eqn]
\tilde{q}^\star = 1a−ib−jc−kd
[/eqn]
interestingly, unlike complex conjugation, quaternion conjugation can be performed using (quat) addition and (quat) multiplication
[eqn]
\tilde{q}^\star = −\frac{1}{2}(\tilde{q}+i\tilde{q}i+j\tilde{q}+k\tilde{q}k)
[/eqn]

>>16726908
this guy gets it. Differential forms are superior in every way

>>16726653
what's a field?
what's a free algebra?
what do you mean by "over"?
what's an indeterminant?
what's a quotient?
how do you arrive at that formula? why exponentiation? why don't they show up in other operations?

>>16726995
equipped with multiplication and conjugation, a norm can be defined
[eqn]
\| \tilde{q} \| = \sqrt{\tilde{q}^\star \tilde{q}}
[/eqn]
(take the time to verify that this satisfies the 3 norm axioms)

>>16726998
go learn linear algebra

>>16726995
all of this can be simplified by saying i^j = - j^i

>>16726999
lastly, with multiplication, conjugation, and a norm, we can now define division as
[eqn]
\tilde{q}^{-1} = \frac{\tilde{q}^*}{\| \tilde{q} \|^2}
[/eqn]
this works as expected, in that if you multiply an quat by its inverse, you get 1.

>>16727008
finally we are in position to prove the rotation formula.
the claim is made that a vector [math]\vec{r}[/math] is rotated about the origin around axis [math]\hat{\vec{n}}[/math] by angle [math]\theta[/math] to vector [math]/vec{r}'[/math] by the quaternion equation
[eqn]
\vec{r}' = \hat{\tilde{q}} \vec{r} \hat{\tilde{q}}^{-1}
[/eqn]
where [math]\hat{\tilde{q}}[/math] is a (unit-norm) quaternion that defined by
[eqn]
\hat{\tilde{q}} = e^{\hat{\vec{n}} \frac{\theta}{2}} = \cos \frac{\theta}{2} + \hat{\vec{n}} \sin \frac{\theta}{2}
[/eqn]
subject to the constraint that the axis is a unit vector
[math]\| \hat{\vec{n}} \| = 1[/math]

>>16727017
putting it all together, here comes the big ugly proof (less one lemma which i'll post in a moment)
[eqn]
\begin{align}
\hat{\tilde{q}} \vec{r} \hat{\tilde{q}}^{-1}
&=
\left[\cos \frac{\theta}{2} + \hat{\vec{n}} \sin \frac{\theta}{2}\right]
\vec{r}
\left[\cos \frac{\theta}{2} - \hat{\vec{n}} \sin \frac{\theta}{2}\right] \\
&=
\vec{r} \cos^2 \frac{\theta}{2}
- \vec{r} \hat{\vec{n}} \cos \frac{\theta}{2} \sin \frac{\theta}{2}
+ \hat{\vec{n}} \vec{r} \cos \frac{\theta}{2} \sin \frac{\theta}{2}
- \hat{\vec{n}} \vec{r} \hat{\vec{n}} \sin^2 \frac{\theta}{2} \\
&= \vec{r} \cos^2 \frac{\theta}{2}
+ [\hat{\vec{n}} \vec{r} - \vec{r} \hat{\vec{n}}] \cos \frac{\theta}{2} \sin \frac{\theta}{2}
- [\vec{r} -2 \hat{\vec{n}} [\hat{\vec{n}} \cdot \vec{r}]] \sin^2 \frac{\theta}{2} \\
&= \vec{r} \cos^2 \frac{\theta}{2}
+ 2[\hat{\vec{n}} \times \vec{r}] \cos \frac{\theta}{2} \sin \frac{\theta}{2}
- \vec{r} \sin^2 \frac{\theta}{2}
+ 2 \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}] \sin^2 \frac{\theta}{2} \\
&= \vec{r} \left[\cos^2 \frac{\theta}{2} - \sin^2 \frac{\theta}{2}\right]
+ 2 [\hat{\vec{n}} \times \vec{r}] \left[\cos \frac{\theta}{2} \sin\frac{\theta}{2}\right]
+ \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}] \left[2 \sin^2 \frac{\theta}{2}\right] \\
&= \vec{r} \cos \theta
+ [\hat{\vec{n}} \times \vec{r}] \sin \theta
+ \hat{\vec{n}} [\hat{\vec{n}} \cdot \vec{r}][1 - \cos \theta] \\
&= \vec{r} \cos \theta
+ [\hat{\vec{n}} \times \vec{r}] \sin \theta
+ \hat{\vec{n}} [\hat{\vec{n}} \cdot \vec{r}] - \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}] \cos \theta \\
&= [\vec{r} - \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}]] \cos \theta
+ [\hat{\vec{n}} \times \vec{r}] \sin \theta
+ \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}] \\
\hat{\tilde{q}} \vec{r} \hat{\tilde{q}}^{-1}
&= \vec{r}_\perp \cos \theta + [\hat{\vec{n}} \times \vec{r}] \sin \theta + \vec{r}_\parallel
\end{align}
[/eqn]

>>16727035
the following result was used in the above proof
[eqn]
\begin{align}
\hat{\vec{n}} \vec{r} \hat{\vec{n}}
&= \hat{\vec{n}}[\vec{r} \times \hat{\vec{n}} - \vec{r} \cdot \hat{\vec{n}}] \\
&= \hat{\vec{n}}[\vec{r} \times \hat{\vec{n}}] - \hat{\vec{n}}[\vec{r} \cdot \hat{\vec{n}}] \\
&= \hat{\vec{n}} \times [\vec{r} \times \hat{\vec{n}}] - \hat{\vec{n}} \cdot [\vec{r} \times \hat{\vec{n}}] - \hat{\vec{n}}[\vec{r} \cdot \hat{\vec{n}}] \\
&= \hat{\vec{n}} \times [\vec{r} \times \hat{\vec{n}}] - \hat{\vec{n}} [\vec{r} \cdot \hat{\vec{n}}]\\
&= \vec{r} [\hat{\vec{n}} \cdot \hat{\vec{n}}] - \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}] - \hat{\vec{n}}[\vec{r} \cdot \hat{\vec{n}}] \\
&= \vec{r} - 2 \hat{\vec{n}}[\hat{\vec{n}} \cdot \vec{r}]
\end{align}
[/eqn]

>>16727040
and that's it.
it's shit for intuition, but derives the rotation formula using the bare minimum of concepts.
this gives you enough to code up your own quaternion rotation transformation library.
quats are good for rotations because they don't suffer from gimbal lock when tracing out paths in rotation space, and they have useful interpolation methods with useful properties like spherical interpolation

as for graphics, this is pretty much all you will ever need to know about quaternions.
you use them to represent rotations, but they all get mulched into real matrices at the end of the day when the time to apply the transformation comes.

>>16727005
elaborate. is that wedge product? if so, you'd need more equations. also, i've studied exterior calculus, but don't see the connection quats

>>16726618 (OP)
OP this board is far too one-track minded to ever grasp something like this.

They understand advanced mathematical theorems but not the why. The term is "autism".

If you envision the relationships between quaternions like a physical object like "representation theory" then it'll start to make sense.

It's not like a Rubik's Cube "per se", but it's the same idea.
Turn one side one way and then turn one side the other way.
This sequence of transformations produces the same thing "sometimes", but not always. There's a space where these things commute and the order doesn't matter and a bunch of ones where it doesn't.

The final redpill is (at least appears to be) Octonions. These are neither associative nor commutative but behave like numbers as we understand them.

Here's something weird to chew on:

>all of the number systems are powers of analogous powers of 2
>real (1D)
>complex (2D)
>quaternions (4D)
>octonions (8D)

I don't know why. Neither does anyone.
I have a hunch that it's because the idea of inverses produces the number 2 which is then a corollary to a number of other properties.

>>16726710
>>16726735
>>16726970
They're not just used to represent rotations you rubes. They're a whole number system. They also have broad implications in the theory of relativity.

OP this is why I say don't listen to these people. Ask captain aspberger why an alien object showed up on his front lawn and he tells you that people use it to fuel a nuclear reactor.

>>16726618 (OP)
Maybe try learning some Clifford/Geometric algebra first, where quaternions can then be interpreted as a scalar plus three bivectors, a fully three-dimensional geometric idea.

I had to drop out of studying math a while ago so I forgot a lot, but this is the only thing that made me begin to feel like they made sense, and I've gathered that many other people also feel that way.

https://probablydance.com/2017/08/05/intuitive-quaternions/

https://youtube.com/playlist?list=PLpzmRsG7u_gqaTo_vEseQ7U8KFvtiJY4K&feature=shared

>>16726618 (OP)
Three complex planes sharing the real part. What's so hard to understand?

>>16726735
you cannot lerp a matrix

>>16727156
technically theres a 16-tonion too

>>16727161
>They're not just used to represent rotations you rubes.
the very first thing i said in >>16726970 is
>it is important to note at the outset that rotation using quaternions is a special result, and that quaternions do not encode rotations in general
you have the attention span of a goldfish

>>16727161
>They're not just used to represent rotations you rubes.
Name three applications that don't involve transformation, rotation, or other mappings.

>>16727202
Okay so there are more.

I don't know why or what constitutes a "number system".
I saw the thumbnail of a video that said that it never ends, but someone else said that octonions are the final one because it's the point where anything algebraic stops making sense.

>>16727221
It's the foundation of general relativity.

Expand your mind, minion. If you learn arithmetic and take away that you can use it to count sheep then you're going to be confused and fascinated when you see someone using it to count coconuts.

>>16727313
perhaps learn some math before trying to espouse math
it will make you look less dumb

>>16727317
Feel free to explain why a 16-d number system is valid. Or what it even is. Apparently it's obvious.

It was all of human history minus 500 years ago when Cardano figured out that complex numbers existed, and it mindbroke everyone including one guy so hard that he wrote Alice in Wonderland.

z={(x)⋛i}√|§∆, ∆§|√{i⋛(y)}
I'll be leaving now.

>>16727324
i dunno about 16d whatever you're talking about, but reals, complex, quats, and octinions are the only examples of "finite-dimensional unital real non-associative algebras endowed with a nondegenerate positive-definite quadratic form". you're gonna have to study abstract algebra to appreciate that

>>16727331
I was just quoting him. Apparently it doesn't and it only goes to 8d.

I know half of those. I'll get back to you after I've swallowed the Galois pill and I know what's supposed to be special about quadratic forms.

>>16727313
>[Quaternions are] the foundation of general relativity.
No they're not.

>>16727349
After octonions (O), the next extension in the Cayley–Dickson construction is the sedenions (S)
which are 16D

>>16726998
A semigroup is a set equipped with an associative binary operation.
A monoid is a semigroup with an identity element for the operation.
A commutative monoid is a monoid such that the operation is commutative.
A group is a monoid such that every element has an inverse with respect to the operation.
An abelian group is a group where the operation is commutative.
Sometimes call the operation on an abelian group "addition", in which case we call the group an additive group. We denote the identity element in this case by 0.
A ring is an additive group equipped with a second operation, called multiplication, such that all the nonzero elements from a monoid - which we call a multiplicative monoid.
For each of these structures, a (monoid, group, ring, etc.) homomorphism is a map between two objects having the same structure, which preserves the respective structures.
An endomorphism is a homomorphism such that the domain and codomain are the same.
It can be checked that the collection of group endomorphisms of an abelian group form a ring, with the addition being the induced addition from the abelian group structure, and multiplication being composition.
A module over a ring is an additive group such that each element of the ring defines an endomorphism of the additive group, in such a way that defines a ring homomorphism from the ring to the ring of endomorphisms of the additive group.
>What is a field?
A field is a ring such that the multiplicative monoid is an abelian group.
A vector space over a field is module over that field.
An algebra over a field is simultaneously a vector space over the field as well as a ring, such that the additive structures coincide.
>What do you mean by over?
See above.
>What's an indeterminate?
It's just a element of some set which has no relations to the field, ring, etc. over which you are working.

>>16726998
>>16727409
>What is a free algebra?
A free algebra over a field generated by some set of indeterminates is the smallest algebra over that field contains those indeterminates.
An equivalence relation between two sets is a relation which is transitive, symmetric and reflexive.
The equivalence class of an element, with respect to an equivalence relation, is the set of all elements it is equivalent to.
>What's a quotient?
The map defined by sending an element to its equivalence class is called a quotient map, and often we also call the codomain the quotient of the set by the equivalence relation.
>How do you arrive at that formula?
What formula? All I wrote down was the definition.
>Why exponentiation?
What exponentiation? I never involved the exponential map.
>Why don't they show up in other operations?
Why don't what show up? What the fuck are you even talking about, you dipshit? Try asking a well-formed question.

>>16726618 (OP)

Think the Father, Son, The Holy Spirit, and the identity operator in Chris Langan's CTMU. "Multiplication" is the interaction of the 2 elements you are multiplying in the Life Force and Terryen Wave Fields, see Terrence Howard.

>>16727412
>What exponentiation?
He is referring to exponentiating the vector part to get unit quaternions.

>>16727137
[math]
\begin{equation}
e_i \wedge e_j = \frac{1}{2}(e_i \otimes e_j - e_j \otimes e_i)
\end{equation}

Lets negate the equation

\begin{equation}
\begin{split}
-e_i \wedge e_j &= - \frac{1}{2}(e_i \otimes e_j - e_j \otimes e_i) \\
-e_i \wedge e_j &= \frac{1}{2}(-e_i \otimes e_j + e_j \otimes e_i) \\
-e_i \wedge e_j &= \frac{1}{2}(e_j \otimes e_i - e_i \otimes e_j) \\
-e_i \wedge e_j &= e_j \wedge e_i
\end{split}
\end{equation}

Vector multiplication is defined in geometric algebra to be

\begin{equation}
\begin{split}
V^\mu U^\nu & = V^\mu \cdot U^\nu + V^\mu \wedge U^\nu \\
& = scalar + bivector
\end{split}
\end{equation}

Expanding the bivector basis using i j k as x y z directions, then substituting using i $\xrightarrow{}$ j $\xrightarrow{}$ k convention

\begin{equation}
\begin{split}
V^\mu U^\nu & = V^\mu \cdot U^\nu + A i \wedge j + B i \wedge k + Cj \wedge k\\
V^\mu U^\nu & = V^\mu \cdot U^\nu + A k + B j + C i\\
V^\mu U^\nu & = V^\mu \cdot U^\nu + C i + B j + A k\\
\end{split}
\end{equation}

There is a minus sign that was contracted into the scalar B.

A quaternion is therefore a special case of differential k vectors that is obtained by combining a scalar and a bivector (Geometric vector multiplication)
[/math\

>>16727137
>>16727704
[math]
\begin{equation}
e_i \wedge e_j = \frac{1}{2}(e_i \otimes e_j - e_j \otimes e_i)
\end{equation}

Lets negate the equation

\begin{equation}
\begin{split}
-e_i \wedge e_j &= - \frac{1}{2}(e_i \otimes e_j - e_j \otimes e_i) \\
-e_i \wedge e_j &= \frac{1}{2}(-e_i \otimes e_j + e_j \otimes e_i) \\
-e_i \wedge e_j &= \frac{1}{2}(e_j \otimes e_i - e_i \otimes e_j) \\
-e_i \wedge e_j &= e_j \wedge e_i
\end{split}
\end{equation}

Vector multiplication is defined in geometric algebra to be

\begin{equation}
\begin{split}
V^\mu U^\nu & = V^\mu \cdot U^\nu + V^\mu \wedge U^\nu \\
& = scalar + bivector
\end{split}
\end{equation}

Expanding the bivector basis using i j k as x y z directions, then substituting using i $\xrightarrow{}$ j $\xrightarrow{}$ k convention

\begin{equation}
\begin{split}
V^\mu U^\nu & = V^\mu \cdot U^\nu + A i \wedge j + B i \wedge k + Cj \wedge k\\
V^\mu U^\nu & = V^\mu \cdot U^\nu + A k + B j + C i\\
V^\mu U^\nu & = V^\mu \cdot U^\nu + C i + B j + A k\\
\end{split}
\end{equation}

There is a minus sign that was contracted into the scalar B.

A quaternion is therefore a special case of differential k vectors that is obtained by combining a scalar and a bivector (Geometric vector multiplication)
[/math]

>>16727704
>>16727705
well rip. copy the latex and put it in overleaf

>>16727137
Fixed

Wedge product is defined as

[math]
e_i \wedge e_j = \frac{1}{2}(e_i \otimes e_j - e_j \otimes e_i)
[/math]

Lets negate the equation

[math]
-e_i \wedge e_j = - \frac{1}{2}(e_i \otimes e_j - e_j \otimes e_i) \\
-e_i \wedge e_j = \frac{1}{2}(-e_i \otimes e_j + e_j \otimes e_i) \\
-e_i \wedge e_j = \frac{1}{2}(e_j \otimes e_i - e_i \otimes e_j) \\
-e_i \wedge e_j = e_j \wedge e_i
[/math]
Vector multiplication is defined in geometric algebra to be

[math]
V^\mu U^\nu = V^\mu \cdot U^\nu + V^\mu \wedge U^\nu \\
= scalar + bivector
[/math]

Expanding the bivector basis using i j k as x y z directions, then substituting using i $\xrightarrow{}$ j $\xrightarrow{}$ k convention

[math]
V^\mu U^\nu = V^\mu \cdot U^\nu + A i \wedge j + B i \wedge k + Cj \wedge k\\
V^\mu U^\nu = V^\mu \cdot U^\nu + A k + B j + C i\\
V^\mu U^\nu = V^\mu \cdot U^\nu + C i + B j + A k\\
[/math]

There is a minus sign that was contracted into the scalar B.

A quaternion is therefore a special case of differential k vectors that is obtained by combining a scalar and a bivector (Geometric vector multiplication)

>>16727465
I didn't mention that anywhere in my posts. In general, there might not be such an exponential map.

>>16727202 >>16727313
octonions are "the end" because from sedenions(the 16D ones) & up they have zero divisors

>>16727324
>and it mindbroke everyone including one guy so hard that he wrote Alice in Wonderland.
no, apparently the quaternions where the inspirations for the mad hatter scene, other than that i don't know of any qualms that liddle had with complex numbers

>>16727045
Thank you for your service.

>>16726653
Ty makes sense
>>16726998
retard

>>16727985
>In general, there might not be such an exponential map
What? There is always the exponential map to unit quaternions. It's the exponentiation of the Lie algebra [math]\mathfrak{sp}(1)[/math].

>>16728103
There isn't necessarily such a map, e.g. in positive characteristic.

>>16728202
>muh finite characteristic
Only autists care about non-zero char.

>>16728322
Okay? Why are you even responding to my posts?

>>16728374
You have autism.

>>16727375
Yes they are. They're a non-commutative algebra representing the degrees of freedom of 3+1 dimensional space.

>>16728996
You have to be retarded or ignorant
GR is based on tensor calculus. Differential forms are a special case of tensor calculus. Quaternions are a special case of differential forms for 3 dimension only.
see >>16727714

>>16729125
What do you get from tensors that you dont get from clifford/geometric algebra?

>>16729468
they both can be built from the ground up but technically geometric algebra is a special case of tensor algebra as the wedge product is defined using the tensor product
>What do you get from tensors that you dont get from clifford/geometric algebra?
Riemann curvature tensor
Overall geometric algebra is easier to work with despite being an advanced topic due to its algebraic properties

>>16729468
>>16729510
niggers, the more ways you can talk about the same thing, the better
there isn't a best formulation, there are just different formulations with different strengths and weaknesses when applied to different problems.
having multiple ways to think about the same mathematical topic is never a bad thing

>>16729515
read my post again retard
>>16729510

>>16727313
holy fuck you're a retard.

>>16726799
I've been on /sci/ since 2018 and I literally have never seen them clear spam from a thread even once

this board might as well be /b/ or /r9k/ with how many advice threads and schizo posters we get

>>16731290
they used to nuke this board all the way down to page 8. idk what made them stop.

>>16731316
>idk what made them stop
i reckon the lack of pay had something to do with it

>chinese ideograph criticism thread gets social credited
>the spam here is up
go ahead you tofu dreg wu mao mod, ban me too