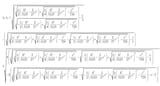
so i'm familiar with the abel ruffini theorem and that polynomials of degree 5 and up can't have general solutions. but what i don't get is how can the roots be algebraic, but not solvable by radicals? aren't those logically equivalent things? surely at some point an algebraic expression has to be closed under radicals right? what else would happen? Do you just have an endless recursive tower of operations that don't converge to the root values? what's the explicit outcome for trying to find the roots on an unsolvable quintic?

>>16727692 (OP)
Reread your question one more time. The exact definition of algebraic numbers is that they're numbers which correspond to roots of polynomials with integer coefficients.

If a polynomical cannot be solved with radicals, then logically there must exist algebraic numbers which aren't an expression of radicals.

>>16727692 (OP)
>>16727731
Here's a better answer:
>https://www.quora.com/What-is-an-example-of-an-algebraic-number-that-cannot-be-expressed-using-radicals

Amit is a fag, but he's correct here.

>>16727692 (OP)
our axioms dont allow it for now.

we still believe 2 negatives equal a positive lmao

>>16727692 (OP)
What makes radicals desirable? You can get exact computer arithmetic for a few more operations https://hackage.haskell.org/package/cyclotomic-1.1.2/docs/Data-Number-RealCyclotomic.html but I'm afraid it's still quite limited so it must be a theoretical interest?

>>16727742
I don't see the part where he proves that the number in question cannot be expressed in radicals. just because there is no general formula for the roots of a polynomial of degree five, it does not yet follow that there aren't various formulae for every polynomial in turn, which aren't special cases of a single formula. for instance x^5-x^4-10*x^3+10*x^2+x-1 has roots expressible by radicals. the nitwit in that quora reply just reiterates the misunderstanding that no root of no polynomial of higher degree than 4 can be expressed using roots just because there is no _general_ such formula. it is unclear why does he even give an example of a polynomial if he then does not do anything with it. his fucked-up "reasoning" does not need an example.

>>16728297
the result is exact, it can be used in further calculations without a loss of accuracy, and later calculations might even get rid of the radicals. once you go 1.4142135, you'll not recover 2.

>>16727692 (OP)
>I’m familiar with the Abel-Rufini theorem
>but I don’t get the Abel-Rufini theorem
So you’re not familiar with the Abel-Rufini theorem. The key observation is that the alternating groups A_n are simple for n>4.

>>16728321
but why does a simple group not have normal subgroups that can encapsulate solving by radicals in finite steps? or better yet, why would it imply it would take an infinite amount of steps and not converge to a valid solution? that's the problem i'm having.

>>16728323
>why does a simply group not have normal subgroups
Because that’s the definition, idiota.

>>16728326
except it still has the trivial subgroup and improper subgroup, so it's not a proper constraint.

>>16728321
That's not an explanation

>>16728307
What exactly is the problem then? To be more explicit, no the properties of being algebraic and expressible using radicals are not equivalent. Proving this is the entire point of why Galois theory was created.

>>16728330
Jesus, do I have to spell it out of you? A simple group is a group that had no PROPER normal subgroups. Are you trolling or just retarded.
>>16728332
Yes, it isn’t. It’s the key fact behind Abel-Rufini that tells you why it’s deg 5 and above. Go learn about Galois groups.

>>16727692 (OP)
>how can the roots be algebraic, but not solvable by radicals
"Roots" are by definition algebraic. Algebraic numbers are those which are roots of polynomials (with whole coefficients).
The point about unsolvability is that you can't get an expression for x in terms of arithmetic operations and root-taking. If you apply the techniques for degree 4, you'll "reduce" a 5th degree to a 6th degree equation, and so on. So yeah, it kind of leads to an endless tower. But you can solve quintics if elliptic functions are allowed, for example.