>>16726105
Well l1 penalty is not special in that sense, the same logic applies to sub-linear penalties as well, e.g. using |x|^p for 0<p<1. These are no longer norms, but they stimulate sparsity more heavily as p decreases, in fact you can use the l0 penalty that counts the number of non-zero entries and this stimulates sparsity the most.
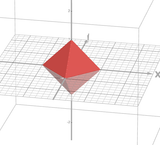
I do think the geometric picture helps actually as to why l1 penalty promotes sparsity. In picrel you can see the l1 ball slopes down somewhat narrowly from its ridges. The unpenalized minimum location is most likely away from the l1 ball and when you introduce penalization and constrain the location to lie in or on the l1 ball, the minimum location will most likely be on the ridges of the ball. This is because the ball slopes down fast from its ridges so if you are going down from the ridge you are changing the coefficients drastically and will not end up at the constrained minimum most likely.

The subgradient has something to do with what I said already. The subgradient of absolute value is step function and so the subgradient is constant, until it flips sign. So you keep making the same steps in the negative direction of the subgradient, regardless of how big the coefficients are, unlike quadratic case where the gradient steps become smaller.