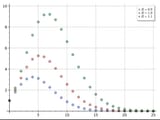
Have you ever heard that the unit n-ball has maximal volume at dimension n = 5? This raises a natural question: what makes the fifth dimension so special? Why does the volume of the n-ball grow with radius until the fifth dimension, and then decrease to zero?

This is because the radius is NOT the natural way to describe an n-sphere. The diameter is. No, this isn't a pithy tau vs. pi debate, it's a very real issue. The n-sphere is contained within an n-cube for any dimension n. The volume of the unit n-cube is unitary at all dimensions.

Imagine a circle in a square. There are four corners of empty space. A sphere inside a cube has 8 corners of empty space. And so on. This tells us the n-sphere, as n grows, takes up less and less space within the cube (in other words, there is more and more empty space in the n-cube). This implies for arbitrarily large n, the volume of the n-sphere goes to zero.

However it doesn't explain the spooky fifth dimension maximal volume for unit radius. The real problem is the argument that the volume of the n-sphere GROWS up until the fifth dimension (or even for non-unitary radius, the volume of the n-ball grows until it hits a peak, and then decreases).

The formula for the n-ball should be written with the diameter. This is because the n-sphere is contained within the n-cube, and it is the diameter of the n-sphere that connects the edges of the n-sphere to the n-cube edges.

When you consider a "unit-sphere" as one of unit diameter (to match the unit-length of the n-cube). you find the that the volume of the n-sphere is monotone decreasing as expected since it is contained within the cube (with the arguments provided earlier).

tl;dr: radius is unnatural descriptor for a sphere; the diameter is the natural measurement for it. A unit n-ball is one with diameter = 1.