>>16722505

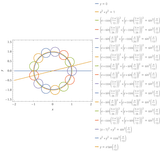
The large yellow circle passes through the centers of the thirteen small circles.

The large blue circle passes through the points of tangency.

(A regular thirteen-gon can be inscribed in the large yellow circle and circumscribed about the large blue circle.)

The angle between the yellow and blue lines is pi/13 radians = 180/13 degrees.
180/13 = 13 + 846153/999999
Which is close to your angle alpha.

The radius of each small circle is sin(pi/13) ≈ 0.2393.
Which is close to your radius of, what appears to be, 0.24.

https://www.wolframalpha.com/input?i=Flatten%5B%7By+%3D%3D+0%2C+x%5E2+%2B+y%5E2+%3D%3D+1%5E2%2C+Table%5B%28x+-+Cos%5B%282+k+%CF%80%29%2F13%5D%29%5E2+%2B+%28y+-+Sin%5B%282+k+%CF%80%29%2F13%5D%29%5E2+%3D%3D+Sin%5B%CF%80%2F13%5D%5E2%2C+%7Bk%2C+13%7D%5D%2C+x%5E2+%2B+y%5E2+%3D%3D+Cos%5B%CF%80%2F13%5D%5E2%2C+y+%3D%3D+Tan%5B%CF%80%2F13%5D+x%7D%5D