I'm working on updating the program now

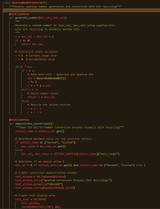
The biggest problem with randomly generating integers for lottery numbers is that lottery numbers are not bit perfect. If they were bit perfert, every lottery number would not exceed 6 or 7 bits. And every lottery number would be 1-63 and 1-127. Those numbers are bit perfect. 63 is exactly 6 bits, and 127 is exactly 7 bits. The current method I've been using with my program is called rejection sampling.

So the problem with lottery numbers that are not exactly 6 or 7 bits is there are left over bits. It inefficient and there's no bit reuse for validly generated bits.

So I'm working on implementing a new method of generating integers with quantum bits. Particularly the bit recycling method, and I'm considering to implement other generation methods as well.

My previous method with sampling rejection was much more simple. It just threw away results with integers that were greater than the max range of the lottery numbers. There was about a 33% rate of rejection.

But a quantum bit that gets generated in my mind, is valid. It shouldn't be thrown away. And there is a way to keep that bit without adding any bias to the randomness of the quantum generator. And it is more computationally efficient than rejection sampling.