Search Results
6/17/2025, 3:19:24 PM
>>105620672
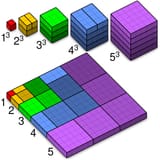
Writing math proofs would help you write proofs of correctness for a program using a proof assistant, like Isabelle or Rocq (which used to be Coq). Or informal proofs of correctness. You basically do really informal proofs by induction to yourself when you envision how and why e.g. a while-loop or a recursive function will eventually terminate and that the desired postcondition will be fulfilled after it terminates. They're really informal in that they're just visual, in the same way this picture is a really informal proof that the sum of a series of cubes (1^3 + 2^3 + ... + n^3) is the same as the square of the sum of a series (1 + 2 + ... + n)^2.
That said, most programming is imperative, so I think leaning stuff like Hoare logic would help more than just pure math proofs.
Writing math proofs would help you write proofs of correctness for a program using a proof assistant, like Isabelle or Rocq (which used to be Coq). Or informal proofs of correctness. You basically do really informal proofs by induction to yourself when you envision how and why e.g. a while-loop or a recursive function will eventually terminate and that the desired postcondition will be fulfilled after it terminates. They're really informal in that they're just visual, in the same way this picture is a really informal proof that the sum of a series of cubes (1^3 + 2^3 + ... + n^3) is the same as the square of the sum of a series (1 + 2 + ... + n)^2.
That said, most programming is imperative, so I think leaning stuff like Hoare logic would help more than just pure math proofs.
Page 1