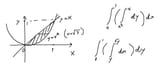In double and triple integrals, I always struggle to define the integration limits.
Why are there 0 and 1 as the limits in this one?
I get x and x2, but for y arent the bounds also defined by the curves rather than actual coordinate axle values?
The bounds can be functions or constants depending on whether the bound is changing. If your upper bound is 5, you're really just saying it's the constant function x = 5.
Both integrals in your screenshot evaluate to 1/6. As long as the bounds are correct, the result will be correct. The reason you would pick one over the other is when setting up the bounds is simpler, like with more complex functions that have uglier inverses or in a different coordinate system. This is a simple problem that you could have solved in Calculus 1 by using the function y = x - x^2 and that's exactly what solving the inner integral puts into the second integral in the first approach. The assumption in Calculus 1 is that you are integrating between the function and y = 0, now we've removed that assumption and we specify the lower bound with a different function. Make more sense now?