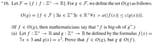>>16691965 (OP)
Before doing the problem you first need to understand the Intuition, for example what is [math]O(g)[/math]? I know it's defined right there but what is that definition really? Intuitively [math]O(g)[/math] is the set of all functions in [math]\mathcal{F}[/math] that grow as fast or slower than [math]g[/math]
What this problem is really asking you is to prove that [math]g[/math] grows faster than [math]f[/math]
At what point does [math]g[/math] outgrow [math]f[/math]? if you plug in some values you will realize this point occurs when [math]x>7[/math] (or [math]x \geq 8[/math] since [math]x[/math] is an integer)
So now we have the intuition we put it into a formal proof:
Assume [math]x \geq 8[/math]
[math]\Rightarrow x^2 \geq 8x \\ \Rightarrow x^2 \geq 7x+x \geq 7x+3 \\ \therefore g(x) \geq f(x) [/math]
This is true for all [math]x>7[/math]. So now set [math]a=7[/math] and [math]c=1[/math] and the condition inside [math]O(g)[/math] is satisfied (absolute value bars can be ignored here since [math]f[/math] and [math]g[/math] are always positive) so [math]f \in O(g)[/math]. This could be alternatively proved by letting [math]c\geq10[/math] then [math]f(x)\leq cg(x)[/math] for all [math]x \in \mathbb{Z}^+[/math].
To prove [math]g \notin O(f)[/math] assume the opposite for a proof by contradiction, so there exists some [math]a \in \mathbb{Z}^+[/math] and some [math]c \in \mathbb{R}^+[/math] such that [math]g(x) \leq cf(x)[/math] for all [math]x>a[/math]
So [math]x^2 \leq c(7x+3)[/math]
[math]\Rightarrow x^2 \leq 7cx+3c < 7cx+4c \leq 7cx+4cx = 11cx \\ \Rightarrow x^2 < 11cx \\ \Rightarrow x < 11c[/math]
And this should be true for all [math]x>a[/math], but it's also obviously false for all [math]x\geq 11c[/math], a contradiction. Therefore [math]g \notin O(f)[/math]