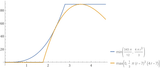
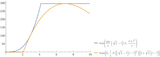
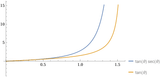
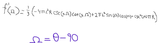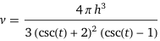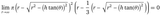>>16754058
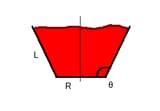
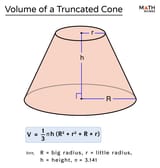
suppose the truncated cone is aligned with the [math]z[/math]-axis and that the base of the cone with radius [math]R[/math] coincides with the [math]xy[/math]-plane.
use the parameterization as described in
>>16749363, with base radius [math]R[/math], side length [math]L[/math], and base angle [math]\theta[/math]
the height of the truncated cone along the axis is [eqn]\Delta z = L \sin \theta[/eqn]
the change in radius from the base to the top is [eqn]\Delta R = - L \cos\theta[/eqn]
the radius as a function of [math]z[/math] is linear, and therefore
[eqn]r(z,\theta) = R + z \frac{\Delta R}{\Delta z} = R - z \cot \theta[/eqn]
integrating the radius as a solid of revolution along the axis gives the volume
[eqn]V(\theta) = \int_0^{\Delta z} \pi r(z, \theta)^2 dz[/eqn]
evaluate this integral
[eqn]
\begin{split}
V(\theta) &= \pi \int_0^{\Delta z} [R - z \cot \theta]^2 dz \\
&= \pi \int_0^{\Delta z} [R^2 - 2 R z \cot \theta + z^2 \cot^2 \theta] dz \\
&= \pi R^2 \int_0^{\Delta z}dz - 2 \pi R \cot \theta \int_0^{\Delta z} z dz + \pi \cot^2 \theta \int_0^{\Delta z} z^2 dz \\
&= \pi R^2 z \bigg|_0^{L \sin \theta} - 2 \pi R \cot \theta \frac{1}{2}z^2\bigg|_0^{L \sin \theta} + \pi \cot^2 \theta \frac{1}{3}z^3\bigg|_0^{L\sin\theta}\\
&= \pi R^2 L \sin \theta - \pi R \cot \theta L^2 \sin^2 \theta + \pi \cot^2\theta \frac{1}{3} L^3 \sin^3\theta \\
&= \pi R^2 L \sin \theta - \pi R L^2 \cos \theta \sin \theta + \frac{1}{3} \pi L^3 \cos^2 \theta \sin\theta
\end{split}[/eqn]
so
[eqn]\boxed{V(\theta) = \pi R^2 L \sin \theta - \pi R L^2 \cos \theta \sin \theta + \frac{1}{3} \pi L^3 \cos^2 \theta \sin\theta}[/eqn]
which, once again, can be simplified a variety of ways using trig identities
for instance, putting everything in terms of sines
[eqn]V(\theta) = \pi R^2 L \sin\theta - \frac{1}{2} \pi R L^2 \sin 2 \theta + \frac{1}{3} \pi L^3 [1 - \sin^2\theta] \sin \theta[/eqn]
all the powers of sine can be reduced to a single powers of sine (with multiples of [math]\theta[/math])