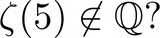Is zeta of 5 irrational?
How do we prove that zeta(5) is irrational? We know zeta(3) is irrational by Apéry's beautiful proof, but how do we extend these two other integers?
Many mathematicians all of zeta(3), zeta(5), zeta(7), .... to be transcendental.
Btw by zeta (n) I mean the Riemann zeta function of n, e.g. zeta(-1)=-1/12, zeta(2) = pi^2\6, zeta(4)=pi^4/90, etc...
Many mathematicians all of zeta(3), zeta(5), zeta(7), .... to be transcendental.
Btw by zeta (n) I mean the Riemann zeta function of n, e.g. zeta(-1)=-1/12, zeta(2) = pi^2\6, zeta(4)=pi^4/90, etc...