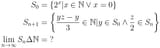Search Results
6/19/2025, 7:14:45 PM
>>16700143
i prefer going in reverse, thinking of the system as branching series of odd numbers multiplied by powers of 2.
because of the way you get new branches (take one of the even parts of the previous sets, subtract one, divide by 3), the process can't create loops at all:
because [math]\frac{n-1}{3}[/math] is the only way to "go backwards," a loop would need either an even number from dividing an odd number by another odd number (impossible; excludes all even numbers as loop targets) or for one odd number [math]m[/math] to have multiple numbers [math]p[/math] such that [math]m=\frac{p-1}{3}[/math] (also impossible).
the 1-4 loop is a special case because 1 is the only solution to [math]3x+1=2^{2}x[/math] - it's the only place where the two operations overlap. in all other cases, [math]2^{2}x>3x+1[/math] (which, in ALL cases using naturals, including for 1, also applies for all powers of 2 of 3 or greater), and in ALL cases using naturals, including for 1, [math]3x+1>2x[/math]. in short, [math]2^2[/math] is the only way to get a loop, and the only loop it gets you is the 1-4 loop.
since by definition this construction hits everything that goes into the 1-4 loop, if you can prove it hits all of [math]\mathbb{N}[/math], you prove both parts of the conjecture simultaneously.
i prefer going in reverse, thinking of the system as branching series of odd numbers multiplied by powers of 2.
because of the way you get new branches (take one of the even parts of the previous sets, subtract one, divide by 3), the process can't create loops at all:
because [math]\frac{n-1}{3}[/math] is the only way to "go backwards," a loop would need either an even number from dividing an odd number by another odd number (impossible; excludes all even numbers as loop targets) or for one odd number [math]m[/math] to have multiple numbers [math]p[/math] such that [math]m=\frac{p-1}{3}[/math] (also impossible).
the 1-4 loop is a special case because 1 is the only solution to [math]3x+1=2^{2}x[/math] - it's the only place where the two operations overlap. in all other cases, [math]2^{2}x>3x+1[/math] (which, in ALL cases using naturals, including for 1, also applies for all powers of 2 of 3 or greater), and in ALL cases using naturals, including for 1, [math]3x+1>2x[/math]. in short, [math]2^2[/math] is the only way to get a loop, and the only loop it gets you is the 1-4 loop.
since by definition this construction hits everything that goes into the 1-4 loop, if you can prove it hits all of [math]\mathbb{N}[/math], you prove both parts of the conjecture simultaneously.
Page 1