Search Results
6/11/2025, 8:18:02 PM
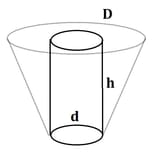
Volume of a cylinder with height h and diameter d: (1/4)(πh)(d^2)
Volume of a partial cone with height h, small diameter d, large diameter D minus the volume of the cylinder above: (1/12)(πh)(D^2+Dd-2d^2)
Assuming h = 8 ft, d = 3 ft, he could safely dig out to a top diameter, D, of approximately 3 2/3 ft (4 inches out from the current aperture), while only filling in the bottom hole to about the 2 ft mark (which, if he does this slowly, is easy to stay on top of). At this point, barring some moderate packing of the sand underneath him, he's now at the bottom of an approximately 6 ft by 3 2/3 ft (ish) hole and can reassess his situation and continue accordingly.
Volume of a partial cone with height h, small diameter d, large diameter D minus the volume of the cylinder above: (1/12)(πh)(D^2+Dd-2d^2)
Assuming h = 8 ft, d = 3 ft, he could safely dig out to a top diameter, D, of approximately 3 2/3 ft (4 inches out from the current aperture), while only filling in the bottom hole to about the 2 ft mark (which, if he does this slowly, is easy to stay on top of). At this point, barring some moderate packing of the sand underneath him, he's now at the bottom of an approximately 6 ft by 3 2/3 ft (ish) hole and can reassess his situation and continue accordingly.
Page 1