Anonymous
10/12/2025, 4:32:27 AM
No.106861598
>>106861648
>>106861673
>>106861714
>>106861768
>>106861798
>>106862015
>>106862179
>>106862209
>>106862281
>>106862302
>>106862715
>>106863388
>>106863477
>>106863695
>>106863740
>>106864586
>>106864615
>>106866990
>>106867856
>>106869373
>>106873107
>>106874661
>>106875041
>>106876103
>>106878022
>>106879303
>>106880067
>>106880297
>>106881239
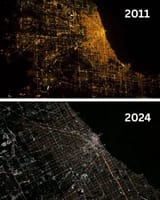
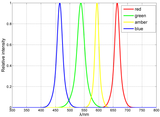
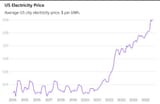
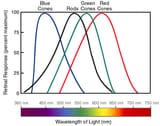
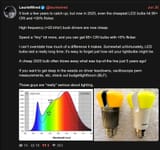
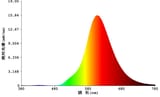
DEATH
Death to LEDs in street lighting